SE1: Kontextfreie Grammatiken

3

Grammatik – formal

Eine Grammatik ist ein 4-Tupel \Gamma = (N, T, \Pi, S) mit einer Menge von Nicht-Terminalsymbolen N, einer Menge von Terminalsymbolen T, einer Menge von Produktionen \Pi und einem Startsymbol S \in N.

N und T sind dabei disjunkt (N \cap T = \emptyset) und endlich. \Pi ist eine endliche Teilmenge von N \times (N \cup T)^*.

Weitere formale Definitionen bitte dem Skript (Vorlesungsfolien), der Wikipedia oder der einschlägigen Fachliteratur entnehmen. Es geht mir hier nicht darum, eine vollständige Abhandlung zu kontextfreien Grammatiken zu liefern, sondern vielmehr auf Fallstricke hinzuweisen und wichtige Details etwas verständlicher zu machen.

Hinweise zu den formalen Definitionen:

  • Eine Grammatik ist ein 4-Tupel, keine Menge. Wichtig sind also, dass es runde statt geschweifte Klammern sind. Das ist wichtig, weil die Reihenfolge entscheidend ist.
  • Die Benennung der einzelnen Mengen ist *nicht* entscheidend (sondern eben die Reihenfolge). Also es kann sein, dass die Menge der Terminalsymbole 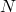N heißt oder das Startsymbol V.
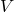  • Die von 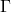\Gamma erzeugte Sprache 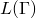L(\Gamma) sollte man nicht mit 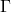\Gamma selbst verwechseln. Insbesondere kann es mehrere unterschiedliche Grammatiken geben, die die selbe Sprache erzeugen.
  • Ein Satz, der syntaktisch nicht korrekt ist, hat per Definition keine Semantik. Selbst dann nicht, wenn man die Bedeutung leicht erraten kann. Compiler raten nicht.

Für was man das braucht

Kontextfreie Grammatiken spielen im Compilerbau eine entscheidende Rolle. Insbesondere sind Programmiersprachen i.d.R. kontextfreie Sprachen. Um also Programmiersprachen zu verstehen kann es nicht schaden, im Groben zu wissen, wie ein Compiler (oder Interpreter) einen Programmtext sieht.

Außerdem kann es in der Praxis schon mal vorkommen, dass man selbst eine kleine Sprache definieren oder analysieren (parsen) muss. Beispielsweise das Format einer Konfigurationsdatei. Oder ein (standardisiertes) Datenaustauschformat. Bei der Definition solcher Formate ist die Erweiterte Backus-Naur-Form (EBNF) weit verbreitet. Und EBNF ist kaum etwas anderes als eine leicht andere Darstellung kontextfreier Grammatiken.

Warum „kontextfrei“?

Kontextfreie Grammatiken heißen „kontextfrei“, weil der Kontext einer Zeichenfolge hier irrelevant ist. Ein deutsches Wort kann verschiedene Bedeutungen tragen, je nachdem, in welchem Kontext es steht (Homonyme, Teekesselchen). Demnach ist die deutsche Sprache nicht kontextfrei.

Man erkennt die Kontextfreiheit an der Form der Produktionen. Bei kontextfreien Grammatiken darf auf der linken Seite nur ein Nichtterminalsymbol stehen. Also insbesondere keine Terminalsymbole und nicht mehr als ein Nichtterminalsymbol. Wäre das der Fall, könnte man die Regel nur anwenden, wenn ein Nichtterminalsymbol im Kontext der anderen Symbole stände. Hier ein Beispiel für eine Regel, die nicht kontextfrei wäre: tA \rightarrow tt. A lässt sich in so einem Fall nur dann zu t ableiten, wenn es auf ein t folgt.

Da es kontextfreie Grammatiken gibt, liegt der Schluss nahe, dass es auch kontextabhängige Sprachen gibt. Und das ist in der Tat so. Der Linguist Noam Chomsky (übrigens eine sehr interessante Persönlichkeit) hat zur Klassifikation formaler Sprachen die so genannte Chomsky-Hierarchie aufgestellt. Kontextfreie Grammatiken entsprechen den Typ-2-Grammatiken der Chomsky-Hierarchie. Weiteres hierzu in der Vorlesung „Formale Grundlagen der Programmierung“.

Was heißt das jetzt intuitiv?

Eine Grammatik beschreibt den syntaktischen Aufbau einer Sprache. Die Terminalsymbole beschreiben hierbei die elementaren Bestandteile, aus denen die Sprache zusammengesetzt ist. Das sind z.B. Ziffern und Buchstaben, können aber auch zusammengesetzte Symbole wie >= oder Schlüsselwörter wie \text{if} sein.

Nichtterminalsymbole beschreiben größere „Einheiten“ einer Sprache. Ein if-Konstrukt könnte beispielsweise durch ein Nichtterminalsymbol beschrieben werden. Eine passende Produktion könnte folgendermaßen aussehen: IfKonstrukt \rightarrow \text{if } BoolAusdruck \text{ then } Ausdruck \text{ else } Ausdruck wobei \text{if, then, else} \in T und IfKonstrukt, BoolAusdruck, Ausdruck \in N.

Die Produktionen sind schließlich die Regeln die beschreiben, wie die Sprache aufgebaut ist, d.h. wie sich die Nichtterminalsymbole als „Einheiten“ in Terminalsymbole aufteilen lassen.

Bei der Analyse des Quelltextes baut der Compiler nun einen so genannten Syntaxbaum auf. Das heißt er fasst Gruppen von Terminalsymbolen zu den genannten größeren „Programmeinheiten“ zusammen. Das ist notwendig um dem Programm eine Semantik zuzuordnen. Also nur, wenn der Compiler weiß „Das hier ist ein if-Konstrukt“, kann er auch passenden Maschinencode generieren. Die Information „Hier steht if“ reicht nicht.

Die Sache mit der Eindeutigkeit

Compiler müssen, wie gesagt, Blöcke aus zusammengehörigen „Programmeinheiten“ bilden. Ein Beispiel:

1
2
3
4
5
if a == b then
if a == 42 then
doSomething;
else
doSomethingDifferent;

Bei so einem Stück Code hat der Compiler zwei unterschiedliche Möglichkeiten der Interpretation:

1
2
3
4
5
if a == b then
  if a == 42 then
    doSomething;
  else
    doSomethingDifferent;

oder

1
2
3
4
5
if a == b then
  if a == 42 then
    doSomething;
else
  doSomethingDifferent;

Die Frage ist also welchem if der else-Block zugeordnet werden muss. Die Grammatik, die der Compiler benutzt, muss darauf eine eindeutige Antwort liefern können, d.h. die Grammatik muss eindeutig sein.

Eine Grammatik ist genau dann mehrdeutig, wenn sie zwei verschiedene Syntaxbäume für den selben Satz hat. Äquivalent dazu ist die Aussage: Eine Grammatik ist genau dann mehrdeutig, wenn die für einen Satz zwei verschiedene Linksableitungen (oder Rechtsableitungen) besitzt. Dabei kann eine eindeutige Grammatik selbstverständlich für einen Satz eine Links- und eine Rechtsableitung haben, die durchaus verschieden sein können. Nur dürfen es keine zwei Linksableitungen bzw. keine zwei Rechtsableitungen sein.

Machen wir mal ein einfaches Beispiel.

Gegeben sei folgende Grammatik:
\Gamma_e = (N, T, \Pi_e, S) mit N = \{ S, A, B \}, T = \{ x, y, z \} und \Pi_e = \{ S \rightarrow AB, A \rightarrow xy, B \rightarrow yz \}

\Gamma_e ist eindeutig und definiert die Sprache, die ausschließlich aus dem Satz xyyz besteht. xyyz hat die beiden Ableitungen
S \Rightarrow AB \Rightarrow xyB \Rightarrow xyyz und
S \Rightarrow AB \Rightarrow Ayz \Rightarrow xyyz

wobei ersteres eine Linksableitung, letzteres eine Rechtsableitung darstellt. Der dazugehörige Syntaxbaum ist gleich:

Zwei gleiche Syntaxbäume

Betrachten wir nun die nicht-eindeutige Grammatik \Gamma_{ne} = (N, T, \Pi_{ne}, S) mit \Pi_{ne} = \{ S \rightarrow AB, S \rightarrow Ayz, A \rightarrow xy, B \rightarrow yz \}

Hier gibt es zwei unterschiedliche Linksanleitungen und zwei unterschiedliche Syntaxbäume:
S \Rightarrow AB \Rightarrow xyB \Rightarrow xyyz und
S \Rightarrow Ayz \Rightarrow xyyz

Zwei Syntaxbäume in einer mehrdeutigen Grammatik

Warum ist aber nun die Grammatik aus dem Skript nun mehrdeutig? Der Syntaxbaum sieht doch fast gleich aus.

Genau das ist der Punkt: Der Baum ist nur fast gleich. In der Vorlesung wurde die folgende Grammatik betrachtet:

\Gamma_{vl} = (\{ S, E \}, \{ ID, *, +, (, ) \}, \Pi_{vl}, S ) mit
\Pi_{vl} = \{ S \rightarrow E, E \rightarrow E + E | E * E | (E) | ID \}

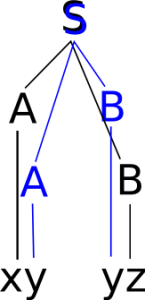
Der betrachtete Syntaxbaum war folgender:

Ableitungsbäume einer mehrdeutigen Grammatik

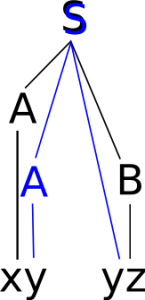
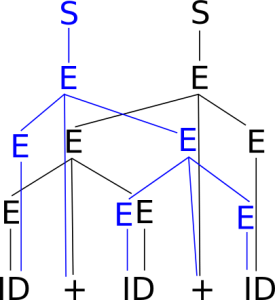
Beim Vergleichen der beiden Bäume dürfen wir den unteren Baum nicht drehen, sondern müssen ihn quasi nach oben klappen:

Die beiden Ableitungsbäume aus der Vorlesung - hochgeklappt

Die beiden Bäume sind zwar sehr ähnlich, jedoch nicht gleich. Genauso lassen sich auch zwei verschiedene Linksableitungen für den gegebenen Satz finden bzw. aus dem Syntaxbaum ablesen:
S \Rightarrow E \Rightarrow E+E \Rightarrow E+E+E \\ \Rightarrow ID+E+E \Rightarrow ID+ID+E \Rightarrow ID+ID+ID
und
S \Rightarrow E \Rightarrow E+E \Rightarrow ID+E \\ \Rightarrow ID+E+E \Rightarrow ID+ID+E \Rightarrow ID+ID+ID

Die Mehrdeutigkeit der Grammatik hat zur Folge, dass nicht klar ist, ob das mittlere ‚ID‘-Symbol nun zum rechten oder linken Teilterm gehört.

Bei der hier gezeigten „Addition“ (wobei Syntax ja noch keine Semantik vorgibt) scheint das nicht weiter von Belang zu sein. Wenn wir jedoch eines der beiden ‚+‘-Symbole durch ein ‚*‘ ersetzen, hieße das, wir könnten nicht entscheiden, ob nun die allseits bekannte Rechenregel „Punkt-vor-Strich“ beachtet wird oder nicht. Und so etwas darf natürlich nicht vorkommen.

Die in der Vorlesung gezeigte mehrdeutige Grammatik ist dahingehend typisch, dass mehrdeutige Grammatiken oft Regeln der Form A \rightarrow AA haben. Solche Regeln führen fast unweigerlich zu Mehrdeutigkeiten Wie im obigen Beispiel die Grammatik \Gamma_{ne} zeigt, sind solche Regeln aber nicht notwendig um mehrdeutige Grammatiken zu basteln.

Hinweis für die SE1-Leute

Das, was ich hier schreibe ist inoffizielles Zusatzmaterial. Es kann euch vielleicht für die Klausur (und/oder darüber hinaus) helfen, aber ihr werdet euch vermutlich nicht darauf berufen können. Im Zweifel gilt nicht das, was hier steht, sondern das Skript bzw. die Vorlesung.

Anmerkungen jeglicher Art sind gerne gesehen. Persönlich, per Mail oder auch als Blog-Kommentar. Wie immer gilt: Bei Fragen: fragen.

3 Kommentare


  1. „S -> Axy -> xyyz“ (Im Beispiel einer n.e. Grammatik)

    Hier ist dir mMn ein kleiner Fehler unterlaufen,müsste es nicht : „S -> Ayz ->xyyz“ heissen?


  2. Gut erkannt. Habs korrigiert. Danke. 🙂

    mfg

    Christian


Schreibe einen Kommentar

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert