Ich hatte vor einiger Zeit versprochen, noch etwas über Parsing zu schreiben bzw. über die prinzipielle Herangehensweise an Parsing-Probleme. Ich bin da selbst kein Experte und hab die zugehörige Vorlesung zum Compilerbau auch noch nicht gehört. Allein schon aus diesem Grund werde ich nicht sehr ins Detail gehen, sondern möglichst einfach einen Überblick geben. Wer mehr wissen möchte, sollte sich in die passende Vorlesung setzen und/oder ein einschlägiges Buch lesen.
Parsing bzw. Compilerbau ist ein sehr gut erforschtes Gebiet der Informatik. Damit beschäftigt man sich schon seit Ewigkeiten. Dementsprechend gibt es da sehr viel Kompliziertes, Detailliertes und auch Nützliches. Der klassische Compilerbau hat sich dabei auf verschiedene Klassifikationen von Grammatiken gestürzt und in der Tat ist das ein Ansatz, der oft sehr hilfreich, weil sehr systematisch ist. In der Praxis will man aber nicht immer einen Compiler schreiben (oder ähnlich komplexe Aufgaben lösen) und so gibt es in der Praxis noch ein paar andere Ansätze, die teilweise ihre Wurzeln zwar ebenfalls im Compilerbau haben, aber dennoch anders funktionieren. Im Folgenden werde ich über alles, was mir so an Ansätzen einfällt, einen Überblick geben und die prinzipielle Herangehensweise erläutern.
Unterschiedliche Aufgaben
Im Umfeld des Parsing gibt es diverse Aufgaben, die jeweils andere Anforderungen und Schwierigkeiten haben. Je nachdem eignet sich der eine oder andere Ansatz besser. Was man so tun kann:
- Entscheiden, ob ein String einer bestimmten Syntax oder Grammatik entspricht
- Einen Quelltext in Maschinencode compilieren
- Einen Quelltext zur Laufzeit interpretieren
- Einen Quelltext von einer Sprache in eine andere Sprache übersetzen (Transcompiler)
- Eine Konfigurationsdatei lesen und speichern
- Ein Dokument lesen und speichern
- Einzelne Wörter durch andere ersetzen
- Die Syntax eines Strings leicht verändern
- …
Neben der konkreten Aufgabe ist natürlich auch entscheidend, wie kompliziert die Syntax ist. Das hört sich nun furchtbar kompliziert an, aber in der Praxis ist es meist relativ leicht den passenden Ansatz zu finden. Zumindest auf dem Niveau, auf dem ich hier diese Aufgaben behandle.
Grammatiken und Parser
Grammatiken bilden die Grundlage für so gut wie alle nicht-trivialen Parsingaufgaben. Wie schonmal erwähnt klassifiziert man Grammatiken grob über die Chomsky-Hierarchie. Typ-0- und Typ-1-Grammatiken sind für Parsingaufgaben her ungeeignet, da sie recht kompliziert sind. Interessanter sind also die Typ-2-, die kontextfreien, und die Typ-3- also regulären Grammatiken. Dabei sind die regulären Grammatiken eine Teilmenge der kontextfreien.
Zu ein und der selben Sprache lassen sich unendlich viele verschiedene Grammatiken finden. Manche dieser Grammatiken sind einfach, andere sind kompliziert. Es gilt also zuerst einmal, eine möglichst einfache bzw. passende Grammatik zu finden.
Reguläre Grammatiken
Reguläre Grammatiken haben nur Produktionen der folgenden Form:
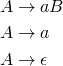
wobei ![]() und
und ![]() mit
mit ![]() . (Es gibt noch alternative Definitionen. Die sind hier aber unwichtig.)
. (Es gibt noch alternative Definitionen. Die sind hier aber unwichtig.)
Anschaulich heißt das, dass bei allen Produktionen auf der linken Seite genau ein Nichtterminalsymbol steht und auf der rechten Seite maximal ein Terminalsymbol gefolgt von maximal einem Nichtterminalsymbol.
Mit dieser Einschränkung der Regeln, ist es möglich, einmal von vorne bis hinten den String einzulesen und dann direkt zu entscheiden, ob es ein Wort der Sprache ist. Insbesondere sind keine komplizierten Rekursionen o.ä. notwendig. Prinzipiell reicht eine Schleife und ein paar if-Anweisungen (in funktionalen Sprachen wie Haskell kommt man natürlich i.A. trotzdem nicht um Rekursion herum). Zu jeder regulären Sprache gibt es einen deterministischen endlichen Zustandsautomaten (DEA), der die Sprache akzeptiert.
Darüber, wie man Automaten nun am besten in Code gießt, lässt sich noch einiges sagen, aber die einfachste Varianten ist die oben erwähnte Schleife mit Fallunterscheidungen für die einzelnen Zustände.
Ein Beispiel:
Gegeben sei die folgende Grammatik, die die Sprache ![]() definiert:
definiert:
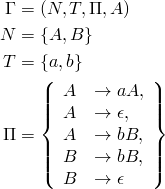
Der zugehörige Automat sieht folgendermaßen aus:
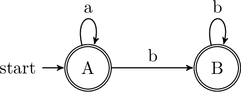
Und hier ein Stückchen Java-Code. In den Kommentaren sind die realisierten Produktionen angegeben.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 | /** Decides whether the given string is a sentence of the gamma language. */ boolean isGammaSentence(String s) { final int A = 0; // an enum would be better; but for simplicity only constants here final int B = 1; int state = A; for (int i = 0; i < s.length(); i++) { switch (state) { case A: if (s.charAt(i) == 'a') // A -> aA state = A; // stay here else if (s.charAt(i) == 'b') // A -> bB state = B; else return false; break; case B: if (s.charAt(i) == 'b') // B -> bB state = B; // stay here else return false; break; default: assert false; // unknown state } } // accept in both states return (state == A) || (state == B); // A -> epsilon; B -> epsilon } |
In jedem Zustand ist beim Lesen des nächsten Zeichens sofort klar, in welchen Zustand als nächstes gesprungen wird. Es gibt immer nur genau eine eindeutige Möglichkeit. Das macht das Parsing regulärer Sprachen relativ einfach.
LL(1)-Grammatiken
Will man eine kontextfreie Grammatik parsen, die nicht regulär ist, muss man auf kompliziertere Parser ausweichen. Es gibt viele verschiedene Arten von Parsern die auf unterschiedliche Art und Weise funktionieren und jeweils andere Teilmengen der kontextfreien Grammatiken parsen.
Eine einfache Parsingmethode nennt sich Parsing durch rekursiven Abstieg. Die zugehörigen Parser und Grammatiken sind die LL(1)-Parser bzw. LL(1)-Grammatiken. Prinzipiell gibt es für jede Produktion eine eigene Funktion, die die Terminalsymbole konsumiert und die Nichtterminalsymbole durch rekursive Aufrufe verarbeitet.
Bei den so genannten LL(k)-Grammatiken ist beim Lesen eines Symbols noch nicht sofort klar, um welche Produktion es sich handelt bzw. was der nächste Zustand wäre. Um das zu entscheiden, muss der Parser ![]() Symbole voraus schauen. Bei LL(1)-Parsern schaut man also genau ein Zeichen voraus. Das wird im Allgemeinen „look ahead“ genannt.
Symbole voraus schauen. Bei LL(1)-Parsern schaut man also genau ein Zeichen voraus. Das wird im Allgemeinen „look ahead“ genannt.
Das folgende Beispiel erkennt die Sprache ![]() durch die Methode des rekursiven Abstiegs. Jede Regel wird durch eine entsprechende Funktion umgesetzt. Da es sich um eine LL(1)-Grammatik handelt, wird an einer Stelle die passende Regel über ein look-ahead-Symbol ermittelt.
durch die Methode des rekursiven Abstiegs. Jede Regel wird durch eine entsprechende Funktion umgesetzt. Da es sich um eine LL(1)-Grammatik handelt, wird an einer Stelle die passende Regel über ein look-ahead-Symbol ermittelt.
Der Einfachheit halber ist das Beispiel prozedural gehalten, was es leicht machen sollte, es in funktionale Sprachen wie Haskell zu übertragen. Ebenso sollte es sich durch Einführen eines String-Attributes leicht objektorientiert lösen lassen.
Zum Parsen wird die folgende Grammatik verwendet:
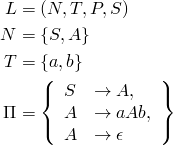
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 | /** Determines if the given String is a valid sentence of the * language {a^n b^n | n in natural numbers} * * The following grammar is used: * L = (N, T, P, S) * N = {S, A} * T = {a, b} * P = {S -> A, A -> aAb, A -> epsilon} */ boolean parse(String s) { assert s != null; // String is valid if everything has been consumed return parseS(s).isEmpty(); } // S -> A String parseS(String s) { assert s != null; s = parseA(s); return s; } // determine rule based on look ahead symbol String parseA(String s) { assert s != null; if (s.isEmpty()) { s = parseAEpsilon(s); } else { char lookAhead = s.charAt(0); if (lookAhead == 'a') { s = parseAaAb(s); } else { s = parseAEpsilon(s); } } return s; } // A -> aAb String parseAaAb(String s) { assert s != null; assert ! s.isEmpty(); assert s.charAt(0) == 'a'; s = s.substring(1, s.length()); // consume 'a' s = parseA(s); // recurse in order to parse a non-terminal symbol if ((! s.isEmpty()) && (s.charAt(0) == 'b')) { s = s.substring(1, s.length()); // consume 'b' } else { return invalidSentence(); } return s; } // A -> epsilon String parseAEpsilon(String s) { assert s != null; // nothing to consume return s; } String invalidSentence() { // This looks like a magic value but it isn't. It's just invalid data that // will not be consumed which results in the parse() function reporting false. // Nevertheless you could argue that this isn't good code -- but it's easy! return "invalid sentence"; } |
Ein größeres Beispiel für einen LL(1)-Parser (allerdings in C++) habe ich vor einiger Zeit auch mal geschrieben. Das Beispiel zeigt neben dem Parser auch einen rudimentären Interpreter für arithmetische Ausdrücke.
Tokenizer
Um die Grammatiken – und damit die Parser – möglichst einfach zu halten, arbeiten Parser für komplexe Sprachen selten direkt auf den Strings, sondern auf so genannten Tokens. Das sind quasi „gruppierte Quelltextblöcken mit Typ“. Schlüsselwörter, Stringliterale, Zahlen, Operatoren und Bezeichner wären Beispiele für Tokens.
Ein vorgeschalteter Tokenizer (auch lexikalischer Scanner oder Lexer genannt) macht aus dem Eingabestring Tokens, die er an den eigentlichen Parser weiter reicht. So würde aus „17+23“ die drei Tokens (Number, 17), (Operator, +), (Number, 23). Die 17 wäre also tatsächlich eine Siebzehn und keine eins und eine sieben.
So vereinfacht sich die Definition der Grammatik beträchtlich. Insbesondere lassen sich so viel leichter LL(1)-Grammatiken finden.
Parsergeneratoren
Insbesondere wenn die Grammatiken kompliziert werden, lohnt es sich, die Parser nicht mehr selbst zu schreiben, sondern schreiben zu lassen. Wie schon erwähnt, ist der Compilerbau stark systematisiert. Und zwar so systematisiert, dass sich hier viel automatisch erledigen lässt. Mit Parsergeneratoren lässt sich aus der Definition einer Grammatik in EBNF automatisch ein Compiler erzeugen, der einen abstrakten Syntaxbaum aufbaut. Oder man spezifiziert neben der Grammatik auch gleich noch ein paar Codefragmente und kann so Interpreter und Compiler automatisch erzeugen lassen.
Fertige Parser
Verwendet man eine verbreitete und vielleicht sogar standardisierte Sprache, die geparst werden soll, so stehen die Chancen gut, dass es dafür bereits Parser gibt, die man nur noch benutzen muss. XML ist ein gutes Beispiel dafür. Normalerweise muss man keinen XML-Parser selbst schreiben. Stattdessen nimmt man sich einen und verwendet ihn einfach.
Manuelles Parsen
In einfach gelagerten Fällen lohnt es sich oft nicht den Ansatz über die Grammatiken zu gehen. Für viele einfache Probleme gibt es deutlich einfachere Lösungen, die sich aber nicht mehr ganz so systematisch konstruieren lassen. Die Sprache der balancierten Klammerausdrücke lässt sich beispielsweise einfach durch Zählen entscheiden.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | /** Checks if the given string is a balanced expression of parentheses, i.e. * every opening parenthesis is closed and every closing parenthesis matches an * opening one. */ boolean isBalancedParenthesisExpression(String s) { int numberOfOpenParentheses = 0; for (int i = 0; i < s.length(); i++) { switch(s.charAt(i)) { case '(': numberOfOpenParentheses++; break; case ')': numberOfOpenParentheses--; break; default: return false; // not a parenthesis } // more closed than opened if (numberOfOpenParentheses < 0) { return false; } } // all parentheses must be closed return level == 0; } |
Hierzu ist eine algorithmische Idee erforderlich, jedoch ist diese Lösung intuitiv verständlich und leicht zu schreiben.
Auf diese Weise kann man auch einfach Sprachen parsen, die von der Theorie her nur sehr schwer zu parsen sein sollten. Die Sprache ![]() ist beispielsweise schon nicht mehr kontextfrei, geschweige denn regulär. Durch einfaches Zählen der Zeichen lässt sich die Sprache aber genau so einfach parsen, als wäre sie regulär.
ist beispielsweise schon nicht mehr kontextfrei, geschweige denn regulär. Durch einfaches Zählen der Zeichen lässt sich die Sprache aber genau so einfach parsen, als wäre sie regulär.
Hier zeigt sich ganz deutlich der Unterschied zwischen Theorie und Praxis. Theoretisch ist es unmöglich, praktisch aber ganz einfach. Genau genommen liegt die Theorie aber nicht falsch. Die Theorie geht eben davon aus, dass ![]() tatsächlich unendlich ist. Da aber alle Datentypen im Rechner beschränkt sind (normalerweise durch eine bestimmte Bitbreite, spätestens jedoch durch den zur Verfügung stehenden – endlichen – Speicher), gibt es also tatsächlich Wörter, die der einfache Ansatz mit dem Zählen der Zeichen, nicht mehr (richtig) erkennt. Nimmt man einem 32-Bit-Integer zum Zählen, wird das Wort
tatsächlich unendlich ist. Da aber alle Datentypen im Rechner beschränkt sind (normalerweise durch eine bestimmte Bitbreite, spätestens jedoch durch den zur Verfügung stehenden – endlichen – Speicher), gibt es also tatsächlich Wörter, die der einfache Ansatz mit dem Zählen der Zeichen, nicht mehr (richtig) erkennt. Nimmt man einem 32-Bit-Integer zum Zählen, wird das Wort ![]() noch richtig erkannt
noch richtig erkannt ![]() jedoch nicht mehr. Die Theorie hat also genau genommen recht. Für die Praxis ist es dennoch (in diesem Beispiel) irrelevant. Denn wer will schon einen String mit mehr als sechs Milliarden Stellen parsen. Zumal dieser String aufgrund seiner Größe schon ganz andere Probleme macht. Strings im Gigabytebereich sind nicht mehr so leicht handhabbar…
jedoch nicht mehr. Die Theorie hat also genau genommen recht. Für die Praxis ist es dennoch (in diesem Beispiel) irrelevant. Denn wer will schon einen String mit mehr als sechs Milliarden Stellen parsen. Zumal dieser String aufgrund seiner Größe schon ganz andere Probleme macht. Strings im Gigabytebereich sind nicht mehr so leicht handhabbar…
Auch beim leichten Verändern von Syntax und beim Auslesen von bestimmten Werten kann so ein Ansatz auf einfachem Weg zum Erfolg führen. Prinzipiell braucht man da kaum mehr als die oben schon verwendete Methode charAt() der Klasse String bzw. in anderen Sprachen etwas entsprechendes. Oft vereinfachen aber weitere Methoden die Arbeit noch weiter. In Java gibt es hier beispielsweise contains(), indexOf(), startsWith(), endsWith(), substring(), replace() und andere.
Reguläre Ausdrücke
Reguläre Sprachen lassen sich nicht nur über reguläre Grammatiken beschreiben, sondern auch über reguläre Ausdrücke (regular expressions, RegEx). RegEx sehen sehr kryptisch aus, sind aber eigentlich ziemlich einfach und erlauben es auf genial einfache Weise, eine Vielzahl von Aufgaben zu erledigen. Für die meisten Sprachen gibt es parser für reguläre Ausdrücke. Teilweise als Zusatzbibliotheken (z.B. in Delphi), teilweise in der Standardbibliothek (z.B. in Java) und teilweise sogar in die Sprache selbst mit eingebaut (z.B. bei Ruby). Der folgende reguläre Ausdruck prüft beispielsweise, ob eine URL valide ist: ^[a-zA-Z0-9-.]*\.[a-z]{2,6}$ [1] Aufgedröselt heißt das:
1 2 3 4 5 6 | ^: Anfang des Strings [a-zA-Z0-9-.]: Die Zeichen 'a' bis 'z', 'A' bis 'Z', '0' bis '9', '-' und '.' *: Diese beliebig oft \.: Dann auf jeden Fall ein Punkt [a-z]{2,6}: zum Schluss die Top Level Domain bestehend aus 2 bis 6 Kleinbuchstaben (von de bis museum) $: Stringende |
Das Suchen und Ersetzen mit regulären Ausdrücken ist bietet weitere vielfältige Einsatzmöglichkeiten; hauptsächlich zum leichten Verändern der Syntax und zum Auslesen von Werten. Viele Editoren haben sogar das Suchen und Ersetzen mit Regulären Ausdrücken als Suchfeature eingebaut, sodass man RegEx nutzen kann um den eigenen Code zu bearbeiten, was insbesondere bei monotonen Codeveränderungen hilfreich sein kann. Das hat dann aber nix mehr mit Parsing zu tun.
[1] Eigentlich müsste man hier noch etwas genauer prüfen. Aber zur Illustration reichts.
Das, was ich hier schreibe ist inoffizielles Zusatzmaterial. Es kann euch vielleicht für die Klausur (und/oder darüber hinaus) helfen, aber ihr werdet euch vermutlich nicht darauf berufen können. Im Zweifel gilt nicht das, was hier steht, sondern das Skript bzw. die Vorlesung.
Anmerkungen jeglicher Art sind gerne gesehen. Persönlich, per Mail oder auch als Blog-Kommentar. Wie immer gilt: Bei Fragen: fragen.
