Das Sortieren ist ein typisches Problem der Informatik. So typisch, dass es mittlerweile dermaßen gut erforscht ist, dass es schon seit mindestens zwei halben Ewigkeiten eine Reihe von Sortieralgorithmen gibt, die quasi jeder Informatiker kennt. Und das obwohl kaum jemand heute noch in der Praxis Sortieralgorithmen schreibt. In der Regel wird ein Problem wie das Sortieren einmal gelöst (d.h. einmal der Algorithmus implementiert) um dann nur noch die bereits bestehende Implementierung zu nutzen. Jede Standardbibliothek für eine x-beliebige Programmiersprache bringt normalerweise einen implementierten Sortieralgorithmus (oft QuickSort) mit, den man dann einfach nur noch benutzt.
Dennoch ist es sehr sinnvoll, die grundlegenden Sortieralgorithmen zu kennen, da diese sehr schön prinzipielle Herangehensweisen an typische Probleme, verdeutlichen. Also auch, wenn man das Sortieren wohl kaum selbst implementieren wird, so wird man ähnliche Algorithmen implementieren, die bestimmte Ideen nutzen, die sich auch in den Sortieralgorithmen finden.
Zu diesen grundlegenden Sortieralgorithmen gehören SelectionSort, InsertionSort, BubbleSort, MergeSort, QuickSort und HeapSort. Diese haben alle gewisse Vor- und Nachteile und zeigen bestimmte Herangehensweisen an algorithmische Probleme.
- SelectionSort ist einfach zu implementieren, intuitiv zu verstehen und minimiert die Anzahl der Zuweisungen (bei Arrays)
- InsertionSort ist ebenfalls einfach und intuitiv und hat außerdem den Vorteil, dass er bereits Sortierte Listen schnell als sortiert erkennt
- BubbleSort ist meiner Meinung nach weniger relevant. Er ist nicht einfacher als SelectionSort und InsertionSort, aber langsamer.
- MergeSort veranschaulicht das Divide-and-Conquer-Prinzip, ist schnell (
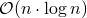 , das ist die Klasse der optimalen Sortieralgorithmen) und lässt sich vor allem auch gut parallelisieren und auf sehr großen Datenbeständen nutzen.
, das ist die Klasse der optimalen Sortieralgorithmen) und lässt sich vor allem auch gut parallelisieren und auf sehr großen Datenbeständen nutzen. - QuickSort ist ebenfalls ein Divide-and-Conquer-Verfahren und meist auch schnell (im average-case
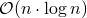 ).
). - HeapSort zeigt schön die Verwendung von bestimmten Datenstrukturen (hier eben einem binären Heap) und ist ebenfalls schnell (
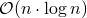 ), jedoch nicht mehr so ganz intuitiv. In der Praxis wird HeapSort u.a. in Prioritätswarteschlangen eingesetzt.
), jedoch nicht mehr so ganz intuitiv. In der Praxis wird HeapSort u.a. in Prioritätswarteschlangen eingesetzt.
Die obige Charakterisierung der einzelnen Algorithmen ist natürlich nicht vollständig und soll nur eine Idee von den Eigenschaften geben. Wie gesagt: Sortieralgorithmen sind sehr gut erforscht und es gibt haufenweise Material dazu im Netz. Hier eine Auswahl:
- Die Wikipedia hat eine ausführlichen Artikel zu Sortieralgorithmen allgemein und zu den einzelne Artikel zu den einzelnen Verfahren: Sortieralgorithmen
- sortieralgorithmen.de zeigt diverse Sortieralgorithmen in unterschiedlichen Varianten teilweise mit graphischer („schöner“, aber nicht unbedingt „anschaulicher“) Visualisierung.
- sorting-algorithms.com hat auch ein paar Visualisierungen
- Noch ein paar schöne Visualisierungen: http://www.gf-webdesign.de/sortieralgorithmen/
- Und weils so schön ist nochmal: http://siebn.de/index.php?page=anisort/anisort. Hier kann man sich sogar sehr schön die einzelnen Schritte ansehen.
- Um HeapSort zu erklären hatte ich ja in der Übung relativ wenig Zeit. Ich hab aber ein schönes Video gefunden, das HeapSort sehr anschaulich erklärt: HeapSort. Das Video ist recht kurz. Damit ein wichtiger Punkt klar wird hier nochmal ein paar Worte dazu:
- HeapSort besteht im Grunde genommen aus zwei Operationen: „Das oberste (größte) Element entnehmen“ und „Heapeigenschaft wiederherstellen“. Letztere ist die interessante Operation.
- Dafür muss man zuerst das größte Element nach oben bringen.
- Danach lässt man alle Elemente, die die Heap-Eigenschaft verletzen, „versickern“, d.h. soweit nach unten wandern, bis die Heap-Eigenschaft nicht mehr verletzt ist.
- Entnimmt man das größte Element oben, dann kann man die beiden Teilbäume nicht einfach zusammenkleben, weil man sonst keinen Binärbaum mehr hätte. Stattdessen wird einfach das letzte Element des Baumes genommen und als Wurzel nach oben gesetzt. Das verletzt zwar wieder die Heap-Eigenschaft (es war ja vorher unten, also kleiner als die oberen), aber es ist „einfach zu erreichen“, d.h. man kann es dem Baum leicht entnehmen ohne, dass man den Baum kaputt macht.
- Bei YouTube finden sich auch noch viele andere Videos zu Sortieralgorithmen, die aber von der Qualität her sehr unterschiedlich sind.
Apropos HeapSort:

Comic CC-BY-NC 2.5 by Randall Munroe
Das, was ich hier schreibe ist inoffizielles Zusatzmaterial. Es kann euch vielleicht für die Klausur (und/oder darüber hinaus) helfen, aber ihr werdet euch vermutlich nicht darauf berufen können. Im Zweifel gilt nicht das, was hier steht, sondern das Skript bzw. die Vorlesung.
Anmerkungen jeglicher Art sind gerne gesehen. Persönlich, per Mail oder auch als Blog-Kommentar. Wie immer gilt: Bei Fragen: fragen.
