Terminierungsbeweise sind generell unmöglich. Im speziellen sind sie aber meist recht trivial und unter anderem müssen das alle SE1-Studenten mal machen. Das Schema hatte ich schon an die Tafel geschrieben und Jenny und Jonas haben es auch mal in digitaler Form verfügbar gemacht: http://sci-nexus.de/project_detail.php?c=1
Hier noch ein paar Hinweise:
- Haltet euch an das Beweisschema: 3 Definitionen, 2 Beweise. Textuelle Begründungen reichen als Beweis nicht aus.
- Der Parameterbereich, für den die Funktion terminiert, ist oft intuitiv ersichtlich. Manchmal (siehe Blatt 8, Aufgabe 2d) werden gewisse Einschränkungen jedoch erst klar, wenn man den restlichen Beweis geführt hat. Es lohnt sich also manchmal, den Parameterbereich nochmals anzusehen.
- Haskell-Datentypen definieren solche Parameterbereiche. Das sind quasi schon Mengen. Mögliche Parameterbereiche sind also beispielsweise:
- die Menge aller ganzen Zahlen bzw. Integer-Zahlen:
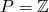 bzw.
bzw. 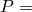
Integer - die Menge der Natürlichen Zahlen
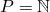
- die Menge aller Integer-Listen:
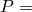
[Integer] - die Menge aller endlichen Listen beliebigen Datentyps
![Rendered by QuickLaTeX.com P = \{ l \in [a] | l \text{ endlich } \wedge \text{ a beliebiger Haskell-Typ}\}](http://www.christian-rehn.de/wp-content/ql-cache/quicklatex.com-c486b394e9177db3efe0dafc1dd95ebb_l3.png)
- die Menge aller Paare aus endlichen Integer-Listen
![Rendered by QuickLaTeX.com P = \{ (a, b) | a, b \in \text{[Integer]} \wedge a, b \text{ endlich} \}](http://www.christian-rehn.de/wp-content/ql-cache/quicklatex.com-866686398ecf11a33ba0370ff90c6932_l3.png)
- die Menge aller Binärbäume von Haskell-Typ
Tree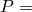
Tree
- die Menge aller ganzen Zahlen bzw. Integer-Zahlen:
- Eine Ordnung
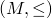 heißt noethersch, wenn jede nicht-leere Teilmenge von
heißt noethersch, wenn jede nicht-leere Teilmenge von 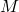 ein minimales Element besitzt. Diese Definition ist äquivalent zu: Eine Ordnung
ein minimales Element besitzt. Diese Definition ist äquivalent zu: Eine Ordnung 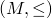 heißt noethersch, wenn jede absteigende Kette irgendwann stationär wird. Letztere Definition finde ich etwas anschaulicher.
heißt noethersch, wenn jede absteigende Kette irgendwann stationär wird. Letztere Definition finde ich etwas anschaulicher. - In den allermeisten Fällen ist
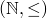 die noethersche Ordnung, die in den Terminierungsbeweisen Verwendung findet.
die noethersche Ordnung, die in den Terminierungsbeweisen Verwendung findet. - In seltenen Fällen (beispielsweise bei der Ackermannfunktion) können auch andere Ordnungen sinnvoll sein. Bei der Ackermannfunktion wäre das beispielsweise
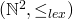 also 2D-Vektoren über
also 2D-Vektoren über 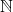 mit lexikographischer Ordnung.
mit lexikographischer Ordnung. - Die
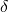 -Funktion muss den selben Definitionsbereich haben, wie die zu untersuchende Funktion. Das sollte man insbesondere dann bedenken, wenn Tupel als Eingabe entgegen genommen werden. Auch, wenn nur eine der Komponenten abnimmt, muss die
-Funktion muss den selben Definitionsbereich haben, wie die zu untersuchende Funktion. Das sollte man insbesondere dann bedenken, wenn Tupel als Eingabe entgegen genommen werden. Auch, wenn nur eine der Komponenten abnimmt, muss die 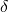 -Funktion das ganze Tupel entgegen nehmen.
-Funktion das ganze Tupel entgegen nehmen. - Eine passende
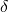 -Funktion findet man meist, wenn man sich die folgende Frage stellt: „Was wird kleiner?“. Das, was kleiner wird, muss die
-Funktion findet man meist, wenn man sich die folgende Frage stellt: „Was wird kleiner?“. Das, was kleiner wird, muss die 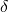 -Funktion zurück liefern.
-Funktion zurück liefern. - Die
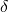 -Funktion ist bei Listen meist, die Funktion, die die Länge der Liste liefert (also
-Funktion ist bei Listen meist, die Funktion, die die Länge der Liste liefert (also length), bei Bäumen meist die Höhe (alternativ, aber u.U. beim Beweis dass die Parameter kleiner werden etwas komplizierter, die Anzahl der Knoten) und bei Integer-Werten die Identitätsfunktion (alsoid). Bei Tupeln kann es auch die Funktion sein, die eine der Komponenten zurück liefert. - Eine
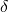 -Funktion kann man mathematisch definieren oder in Haskell-Notation. Letzteres ist meistens einfacher. Die Funktion, die die Höhe eines Baumes berechnet, kann beispielsweise so aussehen:
1
-Funktion kann man mathematisch definieren oder in Haskell-Notation. Letzteres ist meistens einfacher. Die Funktion, die die Höhe eines Baumes berechnet, kann beispielsweise so aussehen:
1
2
3
4data Tree = Leaf | Node Integer Tree Tree
delta Leaf = 1
delta (Node _ a b) = 1 + max (delta a) (delta b)maxist bereits in Prelude definiert und kann daher verwendet werden. - Nehmen mehrere Werte unabhängig voneinander ab (beispielsweise bei
merge), so stellt man je eine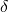 -Funktionen auf und addiert diese. Andere Kombinationen (statt der Addition) wie
-Funktionen auf und addiert diese. Andere Kombinationen (statt der Addition) wie 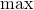 ,
, 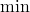 oder die Multiplikation funktionieren in der Regel *nicht*.
oder die Multiplikation funktionieren in der Regel *nicht*. - Das Haskell-Typsystem stellt oft schon sicher, dass der Parameterbereich nicht verlassen wird. Wenn die Funktion nur Integer-Werte entgegen nimmt, wird daraus niemals ein String werden. Es müssen dann nur noch ggf. zusätzliche Bedingungen geprüft werden (z.B.
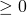 ).
). - Oft ist bei solchen Fällen auch ein Verweis auf das Pattern-Matching angebracht. So kann z.B. für einen bestimmten rekursiven Aufruf gelten, dass ein Parameter
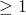 ist, weil der Fall
ist, weil der Fall 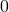 schon im vorherigen Pattern abgefangen wurde.
schon im vorherigen Pattern abgefangen wurde. - Eine häufige zusätzliche Bedingung ist, dass Listen endlich sein müssen (Haskell kann ja auch mit unendlichen Listen arbeiten).
- Man sollte nicht vergessen, dass man *jeden* rekursiven Aufruf prüfen muss.
Und hier noch die Beispiele zum Üben:
-
1
2
3add :: (Integer, Integer) -> Integer
add (x, 0) = x
add (x, y) = 1 + add (x, y-1) -
1
2
3
4ack :: (Integer, Integer) -> Integer
ack (0, m) = m + 1
ack (n, 0) = ack (n-1, 1)
ack (n, m) = ack (n-1, ack (n, m-1)) -
1
2
3
4sum :: [Integer] -> Integer
sum [] = 0
sum (0:xs) = sum xs
sum (x:xs) = 1 + sum ((x-1):xs)
Ihr könnt aber auch quasi jede beliebige Haskell-Funktion nehmen, die ihr mal programmiert habt.
Und hier noch ein paar Lösungshinweise (BTW: Erst selbst versuchen, dann Lösung lesen, nicht umgekehrt!):
- Diese Funktion ist trivial und geht nach „Schema-F“.
- Hier sollte man als noethersche Ordnung
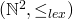 also 2D-Vektoren über
also 2D-Vektoren über 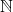 mit lexikographischer Ordnung wählen. Der Rest geht wieder ganz einfach. Man darf sich nur nicht durch die geschachtelte Rekursion durcheinander bringen lassen. Es sind drei rekursive Aufrufe und der geschachtelte liefert einfach einen Wert (nachdem man gezeigt hat, dass dieser terminiert). BTW: Genau genommen müsste noch bewiesen werden, dass
mit lexikographischer Ordnung wählen. Der Rest geht wieder ganz einfach. Man darf sich nur nicht durch die geschachtelte Rekursion durcheinander bringen lassen. Es sind drei rekursive Aufrufe und der geschachtelte liefert einfach einen Wert (nachdem man gezeigt hat, dass dieser terminiert). BTW: Genau genommen müsste noch bewiesen werden, dass 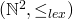 noethersch ist. Das ist aber auch ganz einfach: Sei
noethersch ist. Das ist aber auch ganz einfach: Sei 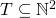 ene beliebige Teilmenge von
ene beliebige Teilmenge von 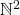 und
und 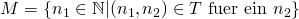 . Dann ist
. Dann ist 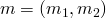 mit
mit 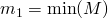 und
und 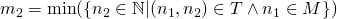 minimal bezüglich
minimal bezüglich 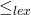 .
. - Bei dieser Funktion (die angeblich mal ne Klausuraufgabe war) muss man bedenken, dass hier quasi zwei Rekursionen gibt, die unabhängig voneinander terminieren. Man könnte versuchen, dafür zwei getrennte Beweise auf zu stellen, aber das halte ich für unsauber. Die Schwierigkeit bei dieser Aufgabe besteht darin, eine passende
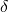 -Funktion zu finden. Hier fragt man sich wieder: „Was wird kleiner?“. Die Länge der Liste wird kleiner. Aber nicht immer. Und das erste Element wird irgendwie kleiner. Aber nicht immer. Das erste Element kann sogar größer werden – nämlich im zweiten Fall (
-Funktion zu finden. Hier fragt man sich wieder: „Was wird kleiner?“. Die Länge der Liste wird kleiner. Aber nicht immer. Und das erste Element wird irgendwie kleiner. Aber nicht immer. Das erste Element kann sogar größer werden – nämlich im zweiten Fall (0:xs). Die Summe der Elemente der Liste wird meistens kleiner. Allerdings nicht, wenn die Liste nur aus Nullen besteht. ==> Des Rätsels Lösung ist die Kombination aus Länge und Summe: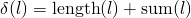
sumkann hier über eine Funktion berechnet werden, die offensichtlicher terminiert, sodass wir hier also nicht in infiniten Regress geraten. Hat man diese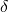 -Funktion, geht der Rest ganz einfach.
-Funktion, geht der Rest ganz einfach.
Update (26.01.11) Hinweise ergänzt und verdeutlicht.
Update2 (28.01.11) Sebastian hat auch noch ein paar Hinweise und Beispiele (auch zu den anderen Beweisverfahren) zusammen gestellt und Jenny hat ein paar Aufgaben gemacht.
Das, was ich hier schreibe ist inoffizielles Zusatzmaterial. Es kann euch vielleicht für die Klausur (und/oder darüber hinaus) helfen, aber ihr werdet euch vermutlich nicht darauf berufen können. Im Zweifel gilt nicht das, was hier steht, sondern das Skript bzw. die Vorlesung.
Anmerkungen jeglicher Art sind gerne gesehen. Persönlich, per Mail oder auch als Blog-Kommentar. Wie immer gilt: Bei Fragen: fragen.
